Corriger le sujet du concours Sonatrach 5
Corriger Controle Module : electronique de puissance avancée
Année d'étude : Master 2 Instrumentation
Exercice #1 :
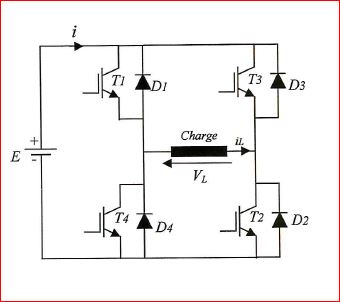
L'onduleur monophasé est montré par la figure ci-contre :
-
Pour le mode de la commande décalée avec un angle, 0 < φ < π, calculer la tension efficace de sortie.
- Cet item demande de déterminer la valeur efficace de la tension à la sortie de l'onduleur lorsque la commande est décalée d'un angle φ par rapport à un signal de référence.
-
Donner le schéma de la génération de la commande MLI à 2 niveaux.
- Ici, on vous demande de dessiner le circuit ou le diagramme qui permet de générer les signaux de commande pour un modulateur de largeur d'impulsions (MLI) à 2 niveaux. Ces signaux seront utilisés pour commander les transistors de l'onduleur.
-
Donner le schéma de la génération de la commande MLI à 3 niveaux.
- De même, pour cette question, il faut représenter le schéma de génération des signaux de commande pour un MLI à 3 niveaux. Ce type de MLI permet d'obtenir une meilleure qualité de sortie (moins d'harmoniques) mais nécessite une électronique de commande plus complexe.
Analyse de l'exercice
Cet exercice porte sur l'étude d'un onduleur monophasé, un convertisseur statique qui permet de transformer une tension continue en une tension alternative. La commande MLI est une technique de modulation largement utilisée pour contrôler la tension de sortie d'un onduleur.
Les points clés à aborder pour résoudre cet exercice sont les suivants :
- Comprendre le fonctionnement d'un onduleur monophasé: Il faut connaître les différents composants (transistors, diodes) et leur rôle dans la conversion d'énergie.
- Maîtriser la notion de commande MLI: Il est essentiel de comprendre le principe de la modulation de largeur d'impulsions et de savoir comment générer les signaux de commande.
- Savoir calculer la tension efficace: Il faut appliquer les formules appropriées pour calculer la valeur efficace d'un signal périodique.
Pour répondre à cet exercice, il sera nécessaire de :
- Analyser le schéma de l'onduleur: Identifier les différents éléments et leurs connexions.
- Établir les équations de fonctionnement: En fonction du mode de commande, écrire les équations qui permettent de calculer les tensions et les courants dans le circuit.
- Dessiner les schémas de génération de commande: Représenter les circuits logiques ou les diagrammes à blocs qui permettent de générer les signaux de commande MLI.
Exercice #2 :
On considère la commande à pleine onde de l'onduleur triphasé avec un amorçage égal à π.
La charge triphasée est purement résistive, R=10 Ω.
- Tracer les tensions Vab et Van.
- Pour les deux types de charge ci-contre, quelles sont les valeurs nécessaires de la tension d'entrée, E pour une puissance de 100 Watts dans la charge.
Analyse de l'exercice
Cet exercice porte sur l'étude d'un onduleur triphasé fonctionnant en mode de commande à pleine onde avec un amorçage spécifique.
Termes clés et concepts :
- Onduleur triphasé: Convertisseur statique permettant de transformer une tension continue en trois tensions alternatives déphasées de 120 degrés.
- Commande à pleine onde: Mode de commande où les transistors de l'onduleur sont commutés de manière à produire des tensions alternatives à partir d'une tension continue.
- Amorçage: Angle de retard par rapport à une référence sinusoïdale à partir duquel un transistor est mis à l'état passant.
- Charge résistive: Charge électrique qui oppose une résistance au passage du courant électrique.
Interprétation des questions :
-
Tracer les tensions Vab et Van:
- Il s'agit de représenter graphiquement les formes d'ondes des tensions entre les phases a et b (Vab) et entre la phase a et le neutre (Van) de l'onduleur triphasé. Ces formes d'ondes dépendront du mode de commande et de la valeur de l'amorçage.
-
Déterminer la tension d'entrée E pour une puissance de 100 Watts:
- Cette question demande de calculer la valeur de la tension continue d'entrée de l'onduleur nécessaire pour obtenir une puissance de 100 Watts dans la charge, en fonction des caractéristiques de la charge et du mode de commande.
Éléments manquants pour une résolution complète :
- Schéma de l'onduleur triphasé: Pour pouvoir tracer les tensions et effectuer les calculs, il est nécessaire de connaître la configuration exacte de l'onduleur (type de transistors, diodes, connexions).
- Type de charge "ci-contre": La question 2 mentionne "les deux types de charge ci-contre" sans préciser de quoi il s'agit. Il faudrait disposer d'un schéma ou d'une description plus détaillée de ces charges.
- Valeur de la tension continue d'alimentation: La tension continue d'entrée de l'onduleur est un paramètre essentiel pour les calculs.
Exercice 3 :
On considère la commande MLI en créneaux avec élimination d'harmonique α₁ < α₂ < α₃ < 90° de l'onduleur schématisé dans l'exercice #1.
- Tracer les signaux de commande et de la tension de sortie.
- Donner le système d'équations à optimiser.
- Écrire les étapes de l'algorithme de Newton-Raphson pour ce système.
Analyse de l'exercice
Cet exercice porte sur une technique avancée de commande d'onduleur : la modulation de largeur d'impulsions (MLI) avec élimination d'harmoniques.
Termes clés et concepts :
- Commande MLI en créneaux: Technique de commande qui consiste à moduler la largeur d'impulsions d'un signal carré pour obtenir une forme d'onde de sortie souhaitée.
- Élimination d'harmoniques: Processus visant à réduire les composantes fréquentielles indésirables (harmoniques) dans le signal de sortie d'un convertisseur.
- Angles d'amorçage α₁, α₂, α₃: Angles de déclenchement des transistors de l'onduleur, permettant de contrôler la forme des impulsions et ainsi réduire les harmoniques.
Interprétation des questions :
-
Tracer les signaux de commande et de la tension de sortie:
- Il s'agit de représenter graphiquement les signaux de commande des transistors de l'onduleur (signaux carrés) et la forme d'onde de la tension de sortie résultante, en tenant compte des angles d'amorçage donnés.
-
Donner le système d'équations à optimiser:
- Cette question demande de formuler mathématiquement le problème d'optimisation qui consiste à déterminer les valeurs optimales des angles d'amorçage pour minimiser certaines grandeurs (par exemple, le taux de distorsion harmonique total).
-
Écrire les étapes de l'algorithme de Newton-Raphson:
- Il s'agit de décrire les étapes de la méthode numérique de Newton-Raphson, qui est souvent utilisée pour résoudre les systèmes d'équations non linéaires issus de problèmes d'optimisation.
Difficultés potentielles et éléments à approfondir :
- Calcul des harmoniques: Il faudra utiliser des outils mathématiques (analyse de Fourier) pour calculer les différentes composantes harmoniques de la tension de sortie.
- Formulation du problème d'optimisation: Il faudra définir une fonction coût à minimiser (par exemple, le taux de distorsion harmonique total) et exprimer cette fonction en fonction des angles d'amorçage.
- Implémentation de l'algorithme de Newton-Raphson: Il faudra connaître les bases de l'algorithme de Newton-Raphson et être capable de l'adapter au problème spécifique.
Pour répondre à cet exercice, il faudra :
- Comprendre le principe de la commande MLI: Savoir comment les signaux de commande influent sur la forme de la tension de sortie.
- Maîtriser l'analyse harmonique: Savoir calculer les différentes composantes harmoniques d'un signal périodique.
- Connaître les méthodes d'optimisation numérique: Savoir utiliser l'algorithme de Newton-Raphson pour résoudre des systèmes d'équations non linéaires.
Exercice 4 :
- Exprimer les lois de commande du cycloconvertisseur à taux d'ondulation six. La tension de référence est V* = Va sin(ωt), avec ω > ωa et ω = 100π.
- Tracer approximativement la tension de charge si ωa = 40°.
Schéma associé : [Image d'un cycloconvertisseur à six impulsions par période avec une charge RL. Les tensions d'entrée V1, V2 et V3 sont indiquées, ainsi que les redresseurs Red1 et Red2.]
Analyse de l'exercice
Cet exercice porte sur le fonctionnement d'un cycloconvertisseur, un convertisseur alternatif-alternatif utilisé pour modifier la fréquence ou la tension d'un système triphasé alternatif.
Termes clés et concepts :
- Cycloconvertisseur à six impulsions: Convertisseur alternatif-alternatif utilisant six thyristors ou IGBT pour réaliser la conversion.
- Taux d'ondulation six: Indique que le nombre d'impulsions par période est de six, ce qui correspond à une fréquence de commutation égale à six fois la fréquence du réseau.
- Tension de référence: Tension sinusoïdale qui sert de référence pour la commande des thyristors.
- Angles d'amorçage ωa: Angles de retard par rapport à la tension de référence à partir desquels les thyristors sont déclenchés.
- Tension de charge: Tension aux bornes de la charge RL.
Interprétation des questions :
- Exprimer les lois de commande: Il s'agit de déterminer les expressions mathématiques qui définissent les instants de commutation des thyristors en fonction de la tension de référence et des angles d'amorçage.
- Tracer la tension de charge: Il faut représenter graphiquement la forme d'onde de la tension aux bornes de la charge RL pour une valeur donnée de l'angle d'amorçage.
Méthodologie de résolution :
- Comprendre le fonctionnement du cycloconvertisseur: Analyser le schéma du circuit et identifier le rôle de chaque composant.
- Établir les équations de commutation: Déterminer les conditions pour que les thyristors conduisent en fonction de la tension de référence et des angles d'amorçage.
- Tracer les diagrammes de commutation: Représenter graphiquement l'état des thyristors en fonction du temps pour différentes valeurs de l'angle d'amorçage.
- Calculer la tension de charge: Utiliser les équations de Kirchhoff et les caractéristiques des composants pour déterminer l'expression de la tension de charge.
Difficultés potentielles :
- Complexité des équations: Les équations de commutation peuvent être assez complexes, en particulier pour les cycloconvertisseurs à plusieurs impulsions par période.
- Représentation graphique: Le tracé des formes d'ondes peut nécessiter l'utilisation d'un logiciel de simulation ou de calcul numérique.
Éléments manquants pour une résolution complète :
- Valeurs numériques des composants: Les valeurs des résistances et des inductances de la charge sont nécessaires pour effectuer des calculs précis.
- Type de charge: Il est important de préciser si la charge est inductive, capacitive ou résistive, car cela influence la forme de la tension de charge.
من هنا : PDF تحميل الحل





تعليقات
إرسال تعليق